🔘 点乘
标签
数学
知识领域/数学
数学/向量
数学/矩阵
数学/点乘
数学/线性代数
数学/高等数学
计算机/计算机图形学
知识领域/计算机图形学
字数
320 字
阅读时间
2 分钟
点乘被用于向量和一维矩阵的计算,点乘的结果是一个值(标量)。
计算公式
向量 a 和向量 b 的每个元素一一对应的进行乘法运算,然后将结果用加法求和。
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影
代码参考
typescript
export function dotProduct(mA: number[], mB: number[]) {
return mA.map((_, i) => mA[i] * mB[i]).reduce((a, b) => a + b)
}结果的几何意义
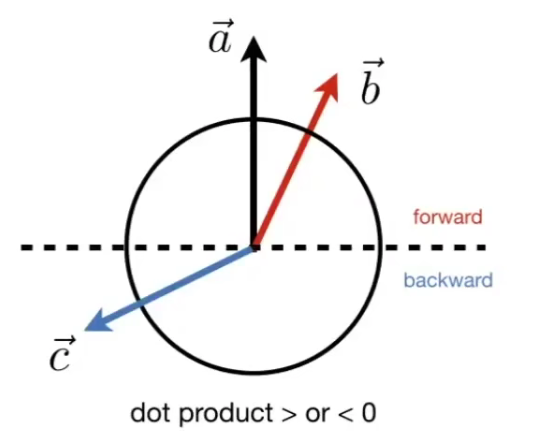
两个向量的方向越接近则值越大,完全同向时值为 1,完全相反时值为 -1,90度夹角时值为 0。可用于判断两个向量之间的距离远近、朝向是否相同。
满足交换律
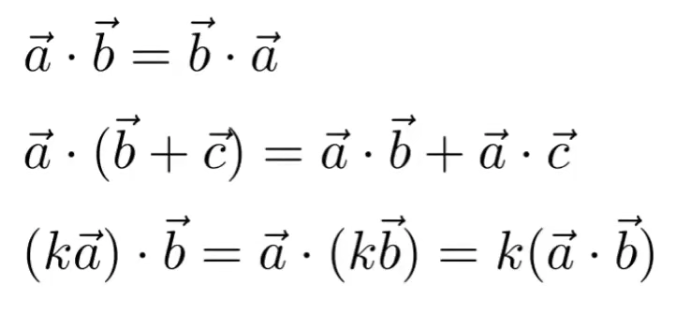
计算向量投影
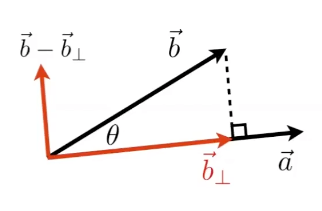
向量 b 到向量 a 的投影称为 , 它的长度(标量投影)公式是:
得出 的向量投影公式:
通过 可以得到 另一个方向上的分量
 絢香猫
絢香猫 絢香音
絢香音